A composite function is a process of combining two or more functions into a single function A function is a representation of work. Let x represent the flour, g(x) represent the function of the food processor in creating the flour dough, and f(x) represent the function of the oven in baking the bread. The output of g(x) should be passed to the function f(x) to make bread (i.e., the prepared dough should be placed in the oven). f(g(x)) is the outcome, which are composite functions f(x) and g(x) (x).
F (x) = logb x is the definition of a logarithmic function. In this situation, the logarithm’s base is b. base and base 10 is the most common base encountered in logs to base 10 and natural logs. Electronics, seismic research, acoustics, and population prediction are all examples of logarithmic uses. Thus, the logarithmic functions with base 10 are called the common logarithmic function and it is denoted by log10 or simply log.
Let us go through some concepts regarding the composite functions and logarithmic functions for better understanding.
Importance of Learning Logarithmic Functions
All students of mathematics should be familiar with logarithmic functions. These functions are an important element of the mathematics curriculum. Logarithmic functions can be used in a variety of domains and for a variety of objectives. As a result, students’ comprehension of this concept has become a necessity. Other reasons to master logarithmic functions include the following:
- Logarithmic functions make calculus, exponents, and other difficult mathematical concepts easier to grasp.
- Logarithmic functions assist you in solving problems involving exponents, integrals, differentiation, and other areas while also helping you to improve your understanding of them.
- You’ll be able to apply the properties of logarithmic functions to a variety of problems once you’ve understood them.
- You can considerably improve your math test scores if you are well-versed in the applications of logarithmic functions.
- You’ll be able to tell the difference between logarithmic and exponential functions if you understand logarithms.
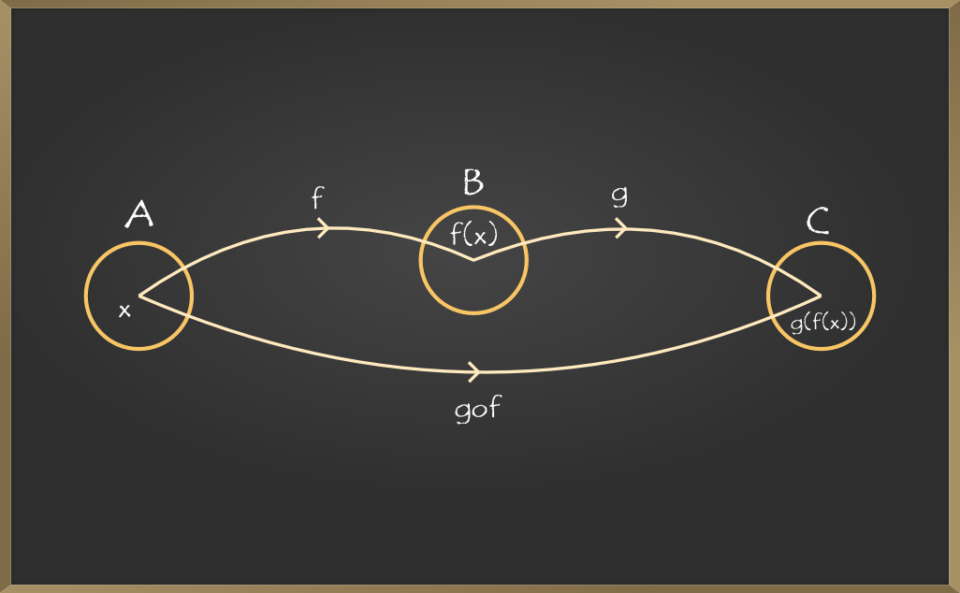
Symbol of Composition of Functions
The function composition’s symbol is. It can also be shown without using this sign and instead of using brackets. i.e.,
- (f g)(x) = f(g(x)) is written as “f of g of x.” The inner function is g, and the outer function is f.
- (g f)(x) = g(f(x)) is written as “g of f of x.” The inner function is f, and the outer function is g.
How to Solve Composite Functions?
We always simplify whatever is within brackets first when using BODMAS. To find f(g(x)), you must first calculate g(x) and then substitute it into f. (x). Similarly, to compute g(f(x)), you must first calculate f(x) and then insert it into g. (x). The order of the composite functions matters, in other words. It means that f(g(x)) might not equal g(f(x)). Using the procedures below, we can get the composite function f(g(a)) for any two functions f(x) and g(x):
- Substitute x = a in g to get g(a) (x).
- Substitute x = g(a) in f to get f(g(a)) (x).
Finding Composite Function From Graph
We should remember that if (x, y) is a point on a function f(x), then f(x) = y to get the composite function of two functions (which are not specified algebraically) illustrated visually. To find f(g(a)) (i.e., f(g(x)) at x = a) using this method:
- First, get g(a) (the y-coordinate on the g(x) graph that corresponds to x = a).
- Find f(g(a)), which is the y-coordinate on the f(x) graph that corresponds to g(a).